
f(x) consists of the square roots of the values in the range of y f(x) for. Make sure both square root functions go over the original graph’s line and then after passing the point where y = 1, descends lower. a) Write an equation for the length of v as a function of h. It would be more useful to select the values so that they are next to the x x value of the. The radical expression end point is (0,0) ( 0, 0). This means that the domain (that is, the set of x-values) for f(x) is all x 0. To find the radical expression end point, substitute the x x value 0 0, which is the least value in the domain, into f (x) x f ( x) x. Where y = 0 on the negative side, 0 on the positive side, 1 and -1. Since f(x) involves a square root, the inputs have to be non-negative. A Square root function contains a square root with the independent variable (x) under the radical.
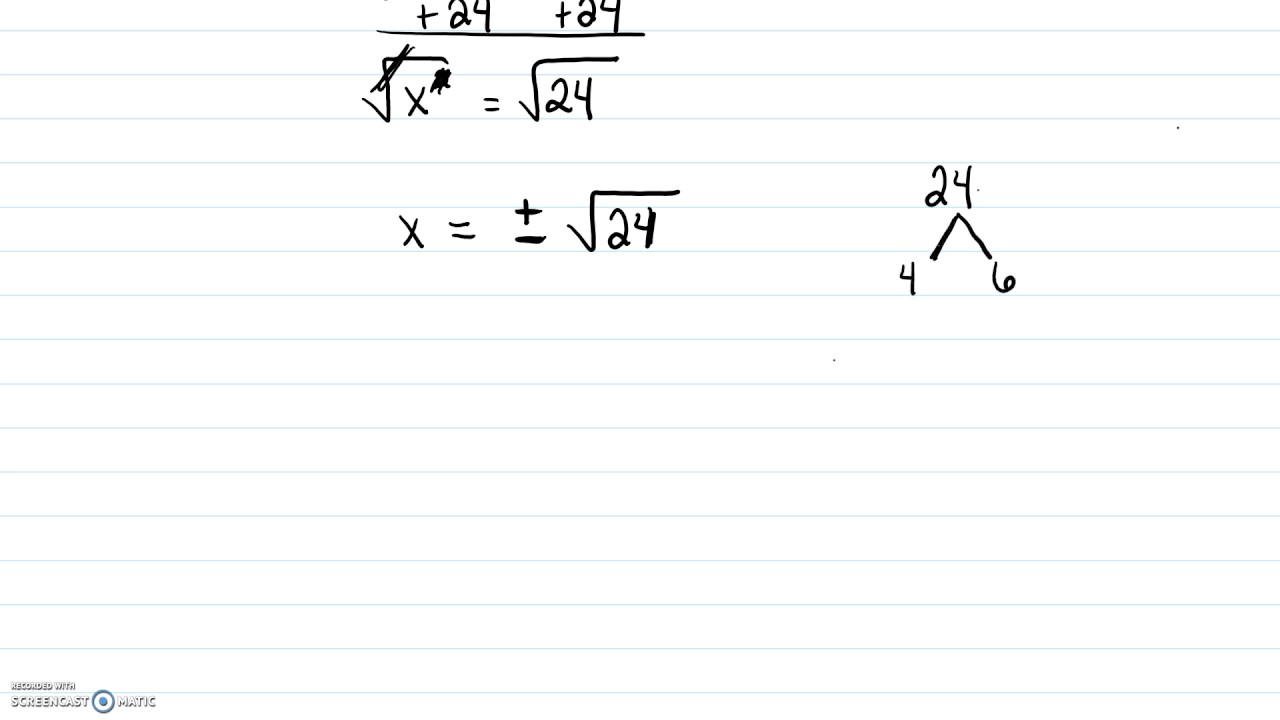
Since this is a parabola now, we are dealing with four invariant points. Square root functions can also be written in h,k form. Afterwards, the function must be lower than the original graph.

With those two points found, we start at the point where y = 0 and go over the original graph’s line to the next point, where y = 1. If you knew the equation for the graph, we could use these two values of y to solve for the two invariant points, but since these points never change, we can just look at the two points on the original graph that have y = 1 and y = 0.

There will always be two invariant points on both graphs where the point does not change. Because each nonnegative real number, x, has precisely one principal square root, x, there is a square root function defined by.


 0 kommentar(er)
0 kommentar(er)
